「5年後に100万円もらえる宝くじ」にいくら払う？ カモられないための正解は…

Finasee（フィナシー）

企業が事業のために資金を調達し、運用するファイナンス。その考え方はビジネスパーソンにとって必須項目なだけではなく、投資にも役立つものです。しかし、ファイナンスについて学びたい……という決意に立ちはだかるのが、難しい数式や計算です。

そんなビジネスパーソンに寄り添うのが、経営者や企業家、コンサル、投資家など最前線のプロたちの意思決定を支えてきたファイナンス理論を石野雄一氏がわかりやすく解説する、話題の書籍『増補改訂版 道具としてのファイナンス』。今回は本書冒頭の序章「ファイナンスの武者修行」、第1章「投資に関する理論」の一部を特別に公開します。（全3回）

●第2回：デキる人は説明できる！「明日の100万円より、今日の100万円が価値が高い」 理由

※本稿は、石野雄一著『増補改訂版 道具としてのファイナンス』（日本実業出版社）の一部を再編集したものです。

5年後に100万円もらえる宝くじの値段

さて、あなたの友人が、「5年後に100万円をもらえるという宝くじ」に当たったとします。この宝くじは国が保証していることから、リスクはないと仮定しましょう。要するに、5年後に100万円が確実に手に入るということです。

すぐにでも、お金が必要な友人は、あなたに「この宝くじを買ってほしい」と依頼してきました。さて、あなたはいったい、いくらで買えば妥当なのでしょうか？ そうです。第1回で出題したクイズです。どう考えればよいのでしょうか？

もしあなたが、「100万円もらえる宝くじなんだから、100万円で買ってあげるよ」と言ったら、友達思いであることはほめられても、ビジネスの世界では確実にカモにされるでしょう。

その理由は、現在の100万円と5年後の100万円とでは、同じ100万円でも価値が異なるからです。つまり、現在の100万円を他の確実な金融商品で運用すれば、向こう5年間で利息を生み出します。

つまり、5年後から見た場合、現在の100万円は「100万円＋利息」の価値を持っているのです。これが「お金の時間価値」といわれるものです。

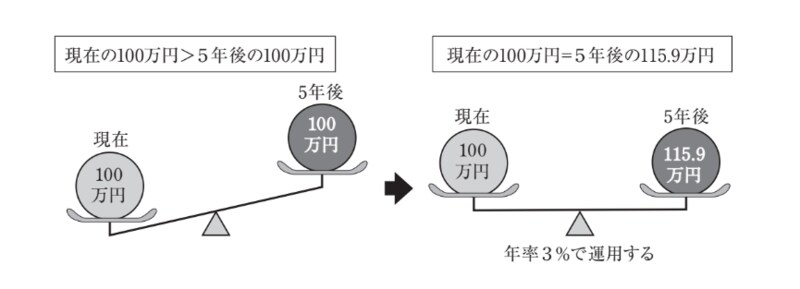
このように、現在の100万円と5年後の100万円とでは、前者の価値が大きいのです。将来価値を学習したあなたなら、現在の100万円の5年後の将来価値の計算方法は、わかっているはずです。

たとえば、現在の5年の定期預金の利率が3%だとしましょう。100万円を定期預金で運用すれば、5年後には100万円×（1＋3%）^5≒115.9万円になります。

ということは、現在の100万円は、5年後の時点では、実は115.9万円の価値があることになります。

逆に、「5年後の115.9万円を年率3%で割り引く ※2（ディスカウントする）と現在の100万円になる」と言いかえることができます。
※2 「100円の商品を10%割引して90円」というお店の割引とは異なります。90円を1年間10%で運用しても100円にはなりません。「割引」の考え方が異なることに注意が必要です。

割引係数をつかって求める「お金の価値」

それでは、5年後の100万円を年率3%で割り引くといくらになるのでしょうか？ 答えは86.3万円=100万円／（1＋3%）^5となります。

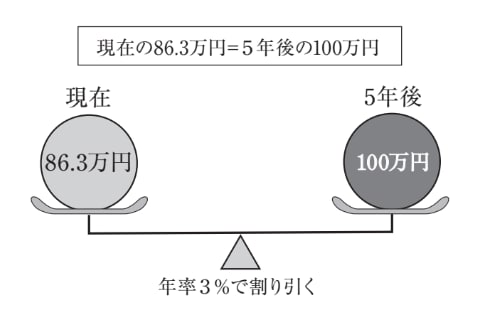
この86.3万円を5年後に受け取る100万円の現在価値（PV：Present Value）といいます。したがって、86.3万円が、あなたが友人の宝くじに払ってもよい上限金額となるのです。

割引率は英語では、ディスカウントレート（discount rate）※3といいます。
※3 この割引率（ディスカウントレート）は、「資本コスト」を基準に決めます。

また、1／（1+r%）^nだけを取り出して、割引係数（DF：Discount Factor）といいます。現在価値を求めるときはn年後に受け取るX円に割引係数を掛けることになります。

将来価値と現在価値の不思議な関係

あなたは5年後の100万円の現在価値を86.3万円と計算しました。このときの割引率は3%です。今度は、86.3万円を年率3%で運用した場合の5年後の将来価値を求めてみましょう。

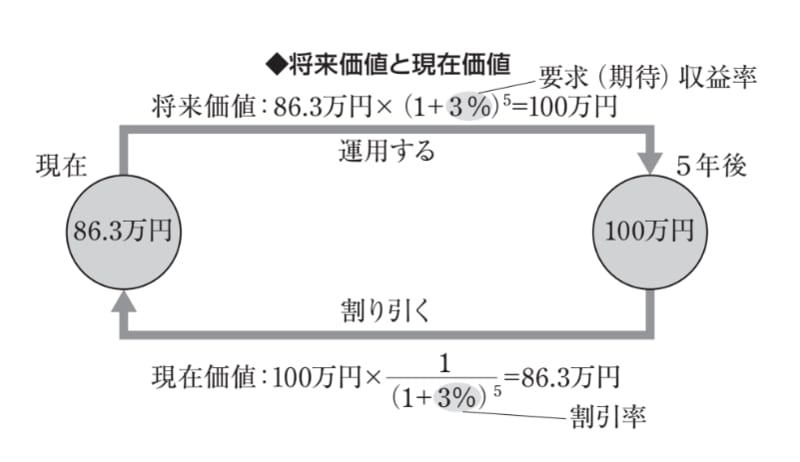
答えは、86.3万円×（1+3%）^5≒100万円となります。86.3万円を割引率と同じ年率3%で運用すれば、5年後には100万円になるわけです。つまり、今日の86.3万円と5年後の100万円の価値が同じであるということです。

現在価値から将来価値を求めるときの利率を要求（期待）収益率といいます。そして、将来価値を現在価値に割り引くとき使うのが割引率（ディスカウントレート）です。

実は、割引率と要求（期待）収益率は表裏一体の関係になっています。ここまでの説明では、割引率（要求収益率）は定期預金の利率3%を使っていました。定期預金のように、5年後にほぼ間違いなく支払われるのと違い、株式に投資した場合のリターンのようにリスク ※4が高い場合は割引率（要求収益率）を高くします。
※4 ここでは「不確実性」と読み替えてください。

リスクが高い投資をするときは、それ相応の高い収益率を要求すべきだからです。これを、ハイリスク・ハイリターンの原則といいます。

次に、割引率を変化させてみましょう。

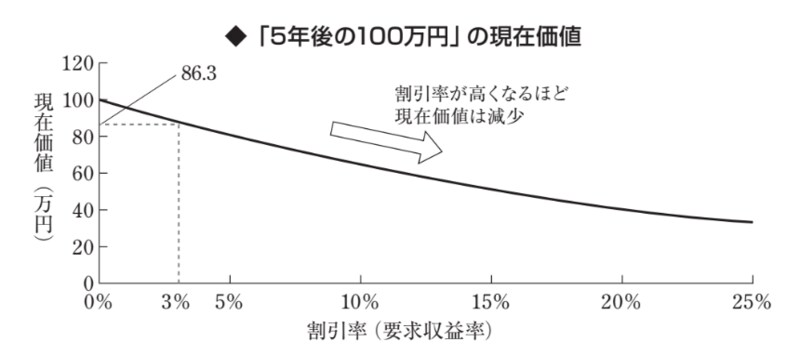
割引率が高くなればなるほど、「5年後の100万円」の現在価値が減少していくことがわかります。この割引率と現在価値の関係は重要です。

『増補改訂版 道具としてのファイナンス』

石野雄一 著
発行所 日本実業出版社
定価 2,750円（税込）

石野 雄一/財務戦略コンサルタント

上智大学理工学部卒業後、旧三菱銀行に入行。9年間の勤務を経て退職後、米国インディアナ大学ケリースクール・オブ・ビジネス（MBA課程）修了。帰国後、日産自動車に入社。財務部にてキャッシュマネジメント、リスクマネジメント業務を担当。2007年より旧ブーズ・アレン・ハミルトン（現：Strategy&）にて企業戦略立案、実行支援等に携わる。2009年に同社を退職後、コンサルティング会社である株式会社オントラックを設立し、企業の投資判断基準、撤退ルールの策定支援、財務モデリングの構築、トレーニングを実施している。著書に『ざっくり分かるファイナンス』（光文社新書）、『実況! ビジネス力養成講義 ファイナンス』（日本経済新聞出版）などがある。