擬似パラドックスのひとつ「ヘンペルのカラス」って何？ ドイツの哲学者が喚起した「結論は正しいけどモヤモヤする証明」をやさしく解説してみた

　今回紹介する、ワダイさんが投稿した『【ゆっくり解説】ヘンペルのカラスは疑似パラドックス』では、音声読み上げソフトを使用して、カラスを用いた「擬似パラドックス」について解説していきます。

---

そもそも擬似パラドックスって何？

魔理沙：
　今回は疑似パラドックスのひとつである、ヘンペルのカラスを解説する。

霊夢：
　疑似パラドックスとは何なのかしら。

魔理沙：
　軽く説明しておくと、パラドックスは正しそうに見える前提と妥当に見える推論から、受け入れがたい結論が得られることをさす言葉だ。

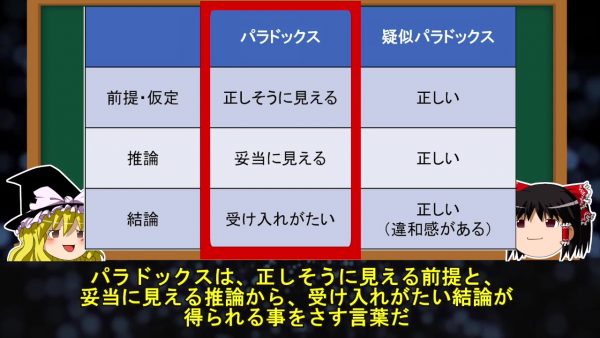
　対して疑似パラドックスは、正しい仮定と正しい推論から、正しい結論を導いたにもかかわらず、結論が直観に反するものを指す言葉なんだ。

　「直観に反するけど結論は正しい」が擬似パラドックスといった感じで覚えておいてくれ。霊夢は「すべてのカラスは黒い」を証明するために、何をしていたんだ？

霊夢：
　私は世界中の黒いカラスを探して見つけようと思っていたのよ。自分の目で見るのが一番だもの。

魔理沙：
　だが現実的にはとうてい不可能だろう。ここでは「対偶論法」という証明法を使い、1羽のカラスも調べずに証明をしてみよう。たとえばネコはネコ科であるという命題があるとする。これは正しいと言えるだろう？ そうであるならば、ネコ科でなければネコではない、と言い換えても真であると言える。

霊夢：
　ネコ科でないネコは、もはやネコじゃないもの。

魔理沙：
　このように「AならばB」に対して、「BでないならばAではない」というように、①命題が正しい時、②命題の仮定と結論を否定した形であっても命題同士が成立する関係性を、対偶というんだ。

　このように命題の真偽が必ず一致する性質を利用した証明法が対偶論法というんだ。この対偶論法は数学など論理的思考で考える世界において証明されている正しい方法だ。

　さて、この対偶論法を使って「すべてのカラスは黒い」を言い換えるとどうなる？

霊夢：
　すべての黒くないものはカラスではないということかしら？

魔理沙：
　そのとおりだ。

霊夢：
　でもすべての黒くないものっていうのは、どういうものをいうの？

魔理沙：
　言葉の通りで黒くないものだ。赤いリンゴや黄色いバナナなどはカラスではないだろう？ すべての黒くないものはカラスではない、の合致例として、赤いリンゴや黄色いバナナなど世界のすべてを調べ上げて、それがカラスではないと証明できれば、すべてのカラスは黒いということを証明できたということだ。

霊夢：
　でも黒いカラスを証明するために、それ以外のすべてを調べるって本末転倒じゃない。

魔理沙：
　すべてを調べ上げるのは現実的ではない。なので確証の原理という、論理的推論を使うことで仮説の確証度を上げることができるんだ。確証の原理とは、さきほどの合致例を見つければ見つけるほど、正しい結論に近づくというものなんだ。

　「すべての黒くないものはカラスではない」に合致するものを1個見つけた時と10個見つけた時なら、どっちのほうがより確証度が高い？

霊夢：
　10個見つけた時のほうが、より自信を持ってすべてのカラスは黒いと言えると思うわ。

魔理沙：
　それが確証の原理の確証度が高いということだ。

霊夢：
　なるほど。調べる数が増えるにつれて、確証度があがるのね。でもここまで聞いてもイメージしづらいわ。

魔理沙：
　ではここまでをイメージしやすいようにたとえてみよう。とある無人島には少年Aがひとりだけで住んでいました。この少年は目に障害があり、黒色だけを認識することができない病気でした。

　この無人島にはほとんどものがなく、あるのはバナナ、水、ゲーム、白鳥、リンゴの5つだけでした。そんなある日、1羽のカラスが無人島に飛んでやってきて少年に言いました。「少年よ、私の色を当てることができるかな」。少年はカラスの声は聞こえるけれど姿は見えません。

霊夢：
　黒色だけ認識することができないから見えないのね。

魔理沙：
　そこで少年は対偶論法を使い、カラスの色を確かめることにしました。バナナ、水を調べると、それはやはりバナナと水でした。次にゲームと白鳥を調べると、やはりゲームと白鳥でした。

霊夢：
　確証度は上がっているわ。

魔理沙：
　少年はほぼカラスは黒色じゃね？ って思ったけど、念のために最後のひとつであるリンゴを調べました。この島のすべてを調べ終えた少年は、この世界の「すべての黒くないものはカラスではない」を確信できたので、カラスの問いに対して黒色だと答えることができました。

　今の例え話のように、限られた世界ならばすべてを調べることはできたが、現実の世界ではできることではないのもわかっただろう？ 正しい対偶論法や確証の原理での証明は、理論上は間違っていないが、なんか違和感があるよねっていうのがヘンペルのカラスの疑似パラドックスなんだ。

　これはドイツ生まれの哲学者であるカール・ヘンペルが指摘し、例としてカラスを使ったことからへンペルのカラスと呼ばれるようになったんだ。

　対偶論法と確証の原理はどちらも正しい証明法なんだが、このふたつから導き出される答えが直感に反する答えになるってのがヘンペルのカラスの疑似パラドックスの面白さだな。

霊夢：
　正しいもの同士を組み合わせると違和感がある答えになるのが不思議ね。

　モヤモヤ風味がまた哲学の面白さを引き出していますね。より詳しい解説をノーカットで楽しみたい方はぜひ動画をご視聴ください。

---

▼動画をノーカットで楽しみたい方は
こちらから視聴できます▼

『【ゆっくり解説】ヘンペルのカラスは疑似パラドックス』』

―あわせて読みたい―

・有名な心理学実験「パブロフの犬」って結局なんだっけ？ 「梅干しを見ると唾液」など“刺激と反応の条件づけ”のメカニズムをやさしく解説してみた

・黒歴史ほど思い出してしまう現象には科学的な裏付けが！ 忘れたいのに消えてくれない記憶のメカニズムと対処法を解説