｢民主主義は数学的にありえない｣選挙で1番人気が当選しても全員が喜べない"本当の理由"

※写真はイメージです - 写真＝iStock.com／bizoo_n

民主主義は最良の政治体制だといわれる。それは本当なのだろうか。元オックスフォード大学教授のキム・ミニョンさんは「残念ながら、すべての人が満足する選挙制度は数学的に存在しない。だが、その困難を克服する方法を見つけ出すというのも数学的な考え方だ」という――。

※本稿は、キム・ミニョン『教養としての数学　数学がわからない僕と数学者の対話』（プレジデント社）の一部を再編集したものです。

■「民主主義は可能か？」という問題を数学的に解く

民主主義とは何でしょうか？

重要な意思決定をするにあたって、社会の構成員の大多数が望む要求をかなえることのできる社会体制と言えばいいでしょうか。

よいと思うことをすべてかなえることができればいいのですが、これは不可能に近いです。各自の要求を並べると、どうしても相互に矛盾が生じますからね。

実際にどのように意思決定をするのかという問題を、数理経済学の視点からまとめた理論があります。これは社会選択理論へと発展し、いまでも活発に研究されている分野です。

その中から、誰もが適切だと思えるような選挙システムをつくることが可能かどうかという問題を扱った、有名な理論を1つ紹介しましょう。もう少し刺激的な表現をするなら、「民主主義は可能か？」という問題を数学的に解いてみましょう。

■1位だけを決める選挙方式に潜む“違和感”の正体

ある学校で学生会長を選ぶとします。候補は、A、B、C、D、Eの5人（図表1）。

イラスト＝『教養としての数学』

選挙権を持った学生は全部で55人です。投票の結果は図表2のようになりました。

『教養としての数学』より

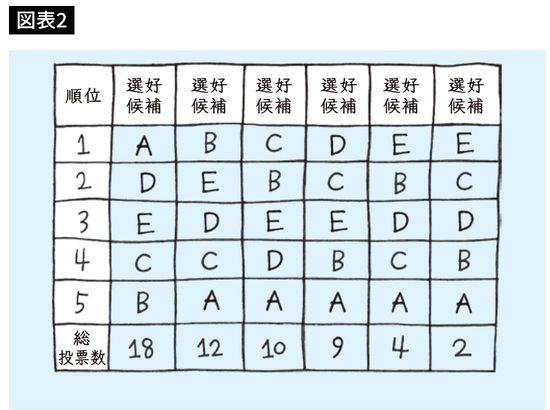
私たちが見慣れている投票結果とはちょっと違いますよね。これは「選好度調査」というもので、社会的決定理論（social determinism）でよく使われるモデルです。

投票用紙に順位が書かれており、各有権者の候補に対する選好度にしたがって1位から5位まで順位を決めるというものです。

この表はA、D、E、C、Bの順で選好度をつけた票が18票、B、E、D、C、Aの順につけた票が12票あったことを意味しています。

現実的にありそうな投票結果よりもかなり単純なデータですが、複雑に見えますよね？

それは問題がより複雑になりそうだということを暗示してもいます。

もし、これが大統領選挙だったら、この選好度の表から見て誰が当選しますか？

一般に私たちになじみのある投票は、1位だけを決めるやり方です。

商品を選ぶときはもちろん、大統領や国会議員の選挙においても、各人の選好度はあるでしょうが、投票ではいつも1人だけ選ぶようになっています。

たとえば大統領選挙であれば、Aが勝つでしょう。

ところで、この表を見てAが勝者にふさわしいと思いますか？

表には6通りの場合の数が出ていますが、はたして誰が選ばれるべきでしょうか？

■多数決で1位でも、選挙方式が変わると最下位に

決選投票をしたとしてもAとDの対決になるでしょうが、他の票を見るとAが選好度の最下位に5回も入っています。

選好度だけで判断するなら、Aは除外されるべきでしょう。

そうして見ると、Bも選好度が低く、平均的にはEの人気がいちばん高そうです。

いまの答えの中にも、さまざまな可能性があります。

いちばん簡単に思いつく方法は、単純多数代表制です。単純多数代表制とは、ただ票を最も多く獲得した、すなわち残りの情報は省略して1位に関する情報だけを反映するものです。

最も簡単ではありますが、すでに1位以外の情報を見た後だと、多数決方式にも問題があるように思えますよね？

多数決方式は便利ですが、昔からその問題点が指摘されています。

アメリカのように多くの州で勝利した人を選ぶ方法もあるでしょうし、選好度に点数をつけて、その合計点で選ぶ方法もありそうです。

たとえば、1位に最も多くの点数を与え、2位以下にはそれより小さい点数を与えていくというように選好度に点数をつける方法です。

18世紀、フランスの数学者で物理学者、政治学者でもあったジャン＝シャルル・ド・ボルダ（Jean Charles deBorda）が初めて考案しました。

彼が考案したボルダ方式（BordaCount Method）は、n人の候補がいると仮定したとき、1位をとった人にn－1点を与え、2位にはn－2点を与え、それ以下も同様の方式で計算するやり方です。

ボルダ方式を使うと誰が勝つのか、もう一度見てみましょう。

この状況では1位は4点、2位は3点、3位は2点、4位は1点が与えられます。

Aの最初の列の点数を計算すると72点ですが、残りの列はすべて0点ですね。なので、Aの得点合計は72点となります。では、すべての結果を見てみましょう。

A　72＋0＋0＋0＋0＝72点
B　48＋42＋11＝101点
C　40＋33＋34＝107点
D　36＋54＋36＋10＝136点
E　24＋36＋74＝134点

直感的に選好度の平均がいちばん高いと思ったEが、Dより低いという結果が出ましたね。でも、DとEの点差はごくわずかなので、ここでDかEかを決めるのは難しそうです。

さらに驚きなのは、多数決では1位だったAが、ここでは最下位になったことです。そこでこう質問することも可能でしょう。これは適切な方法なのでしょうか？

■「誰が選ばれるか」命運を分けるのは“選挙方式”

その質問に答える前に、今度は第3の方法を探してみましょう。

フランスのように決選投票をやってみましょうか。

決選投票では、1回目の投票で誰か過半数を得たら、それ以上は結果が変わらないので、さらに投票する必要はありません。

しかし、誰も過半数を得られない場合はどうするか。その場合は3位以下の候補を除いて、1位と2位で決選投票をします。

ここでは選好度表があるので、もう一度投票をする必要はありませんね。

では、決選投票をしたら、まず誰が落選しますか？

決選投票方式では1位だけを考えるので、他の選好度順位は考慮せず、C、D、Eが落選してAとBが決選に残ります（図表3）。

『教養としての数学』より

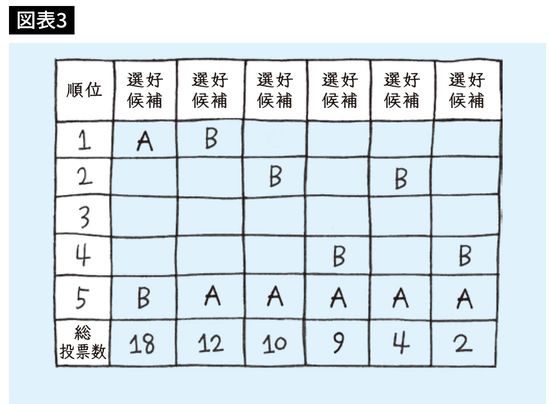
C、D、Eを除いた選好度表を見ると、ほとんどの場合でAよりBの方が上位に来ています。すると、37：18の大差でBが勝つことになります。

ボルダ方式では絶対に勝てなかったBが、ここでは圧勝です。

決選投票をもう少し緻密に発展させた「徹底投票」という方法もあります。

徹底投票とは、過半数を得た候補がいなかった場合、3位以下の候補をすべて除外するのではなく、最下位の候補だけを外しておいて、残った候補でまた投票をする方式です。

誰かが過半数を得るまで、それを繰り返します。では、徹底投票制では誰が選ばれるでしょうか？

この場合、選好度表でいったん誰が1位を多くとったかを見ます。最初のラウンドでは、1位が6票と最も少なかったEが除外されます（図表4）。

『教養としての数学』より

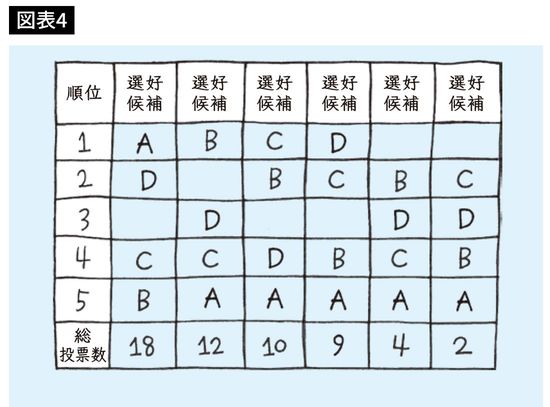
第2ラウンドでは、Eを消した場所に次の順位の者が1位に上がるので、1位の票数が変わります。

Aが18票、Bが16票、Cが12票、Dが9票となりますね。今度はA、B、Cが残りますから、図表5のような結果になります。

『教養としての数学』より

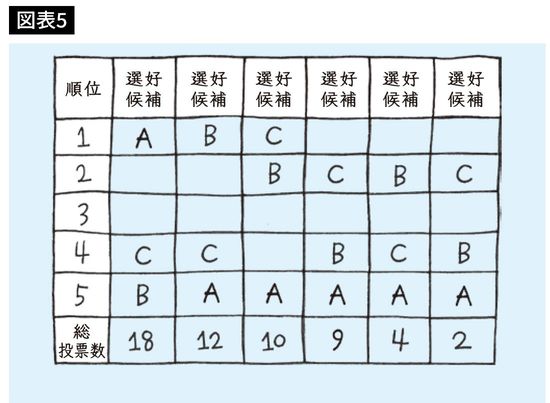
Aが18票、Bが16票、Cが21票となり、かなりはっきりしてきましたが、まだ誰も過半数に達していないので、終わりにはなりません。そこでBを除外すると、Cが勝つことになります。

こうしてみると、投票方式ごとに結果がかなり違いますね。図表17最も一般的な多数決方式ではAが勝ち、ボルダ方式ではD、決選投票ではB、徹底投票ではCが勝ちます。最初に目星をつけたEはまだ一度も勝っていません。

■数学的には誰が当選してもおかしくない

ニコラ・ド・コンドルセ（Nicola de Condorcet）という人がつくった投票方式を利用すれば、また別の結果が出ます。

彼が考案したコンドルセ方式は「一対比較（pairwise comparison）」とも言われます。

何人かの候補のうち2人ずつ組み合わせ、どちらかに投票することを繰り返していきます。そしてすべてのペアを1対1で比較した結果を統合する方法です。

これも一度やってみると、すぐに理解できるでしょう。AからEまで5人の選好度表を見ながら、一対比較をしてみましょう。5人の候補がそれぞれ別の候補と一度ずつ一対比較をするには、何回投票をすればいいでしょうか？

5×4÷2＝10で、10回の投票をすればいいですね。

わかりやすいように、選好度表（図表6）をもう一度見てみましょう。

『教養としての数学』より

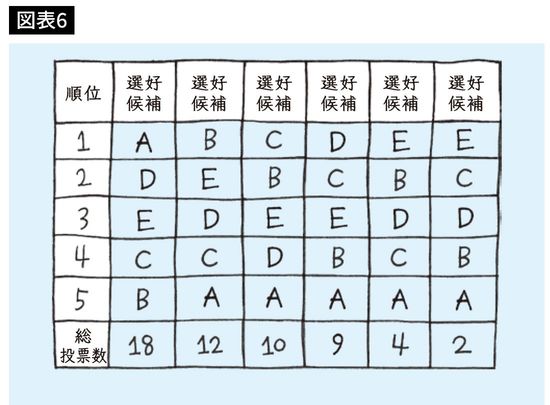
まずAとBを比較すると、どちらが勝つでしょうか？　他の人たちはすべて除いて、2人だけを比べます。BよりAの方が好きな人は18人しかいません。A対Bで見ると、18：37で圧倒的にBの勝ちです。

Aは1対1で比較すると、全員に負けます。

では、Aを除いてB対Cを比較してみましょう。Cを選好する投票は18＋10＋9＋2 ＝39で、CがBに勝ちます。CとDを比べると、Dが43票でDが勝ち、DとEを比べると27：28で僅差ですがEが勝ちます。Eがかなり優勢に見えますね。

E：A＝37：18
E：B＝33：22
E：C＝36：19
E：D＝28：27

上の結果を見ると、1対1で比較したとき、誰と比較してもEの選好度が高いので、Eが勝つことになります。かなり説得力のある論理ではありませんか？

このように誰と比較しても勝つ候補がいる場合、コンドルセ勝者（Condorcet’s winner）と呼びます。そこでコンドルセの原理を「コンドルセ勝者がいれば、その候補が勝つべきだ」と表現することもあります。

1対1の比較をして選好度の高い候補がいれば、その人が勝つべきだということですが、はたしてそんな候補がいるでしょうか？　いないこともあるでしょう。

実際、コンドルセ方式は現実の選挙の方法論とは言いがたいものです。投票したら誰かが勝者にならないといけないのですが、勝者がいないこともあるからです。

つまり、これまで出てきた方法論には、いずれも頭の痛い欠点があるようです。

社会的決定の問題がそれだけ複雑だということが、数学的にも表れています。

■誰もが納得できる選挙に必要な3つの条件

1950年代、社会的決定システムが備えるべき非常に簡単な条件、誰が見ても理解できる3つの原則がつくられました。方法論ではなく、原則を羅列したものです。

第一の原則は、「意見一致の原則」です。もし、すべての人がBよりAを選好するなら、共同決定もやはりBよりAを選好すべきというものです。この第一の原則は、あまりに当然のことですよね。

第二の原則は、先ほどの「計算コンドルセ方式」からくるもので、「独立性の原則」です。これは、AとBの選好度の結果が、他の候補の有無によって変わってはならないというものです。CがいるときはAが勝ったのに、CがいないとBが勝つという状況になれば、社会が個人の合意からなるという理念に反します。

最後の原則は、ある一個人の意見がつねに社会的決定に反映されるような状況があってはならないというものです。投票を左右する「独裁者は存在しない」。この原則はよく理解できます。

意見一致の原則、独立性の原則、独裁者は存在しない。

この社会選択の三原則は、私たちが理性的だと感じる方法論の制約条件です。この原則さえ守れば、すべての人を満足させる方法論をつくることができるでしょう。

■選挙システム自体が抱える、シンプルな矛盾

前で見てきたさまざまな方法論の中から、この三原則に反しないかどうかを基準にして、不適切なものを1つずつ取り除けば、最も適切な方法論が見つかりそうです。

この三原則を考えたのが、1972年にノーベル経済学賞を受賞したケネス・アロー（Kenneth Joseph Arrow）です。

社会的選択理論の最も重要な基盤となる「アローの定理（Arrow’stheorem）」をつくった人です。社会的選択理論の新たなパラダイムを立てた創始者とも言えます。

ところが不幸にも、このアローの定理が物語るのは、「答えがない」という事実でした。「候補が少なくとも3人いる選挙では、この原則を満たす方法論はない」

そのため、彼の定理は「不可能性の定理（impossibilitytheorem）」とも言います。その証明はここでは説明しませんが、この三原則をすべて満たすシステムをつくろうとすると、どうしても矛盾が起こってしまいます。

その矛盾の根本は、たとえばAよりBを選好し、BよりCを選好し、CよりAを選好すれば、序列をつくることができないという、単純なシナリオにあります。この事実も興味深いですね。

■誤った証明や誤った定理だらけの数学史

だとしたら、すでに不可能であることが証明された社会的選択理論を、その後どうやって発展させることができるというのでしょうか？

そう思うのも無理ありません。ですが、科学的な時間から見れば、これは終わった問題ではありません。制約がどこにあるのかを見つけ、その制約を克服する方法を見つけ出すこと。それが数学的な考え方です。

答えをすぐに見つけることはできなくても、どんな答えが条件に合うのかを明確に示すことで、そこに生じる制約を理解して批判しながら、新しい学問分野、研究方向、革命的な視点は生まれます。

いまもアローの定理を改善しようとする研究が多く進められています。

これは単なる理論的問題ではありません。社会的な決定はつねに下さねばならないからです。

数学史を見渡せば、その中には誤った証明や誤った定理がたくさんあります。

ところが、むしろその多くの失敗が現象を理解することに大きな役割をはたしてきました。いかなる制約があるのかを、私たちに確認させてくれたからです。

■「答えがない」から始まる数学的思考法

アローの不可能性定理もまた、答えがないことがわかって終わりではなく、それ以降も研究者たちの指標となってきました。

キム・ミニョン『教養としての数学　数学がわからない僕と数学者の対話』（プレジデント社）

一般的に、社会的選択理論に対して多くの批判があるにもかかわらず、この理論は社会福祉の領域など多様な分野に適用されてきました。

重要なことは、この理論が倫理的なシステムにまったく依存しない点です。

つまり、民主的な観点からも、理性的な観点からも、すべての人が受け入れ可能な原則から始まっているのです。

数学的な思考が社会にどう役立つのかという問いに答えるとき、数という概念に引きずられると、非常に限定的な見方にとらわれてしまいます。

私の考える健全な科学的視点とは「近似（approximation）」していく過程である、これを前提とすることです。

完璧にできないからと諦めるのではなく、限定された条件の下でも理解できる現象があることを受け入れ、後からひっくり返されても、現在の条件の中で可能なかぎり考えることが大切です。

近似していく道のり、つねに変わりうる可能性、そして繊細に論理を組み上げる過程。それこそが学問だと言ってもいいでしょう。

----------

キム・ミニョン 数学者
ソウル大学数学科を卒業し、イェール大学で博士号を取得。マサチューセッツ工科大学研究員、ユニバーシティ・カレッジ・ロンドン（ロンドン大学）教授などを経て、韓国の浦項工科大学（ポステック）教授、ソウル大学客員教授を歴任。2011年に韓国人数学者としてはじめてオックスフォード大学正教授に任用される。「フェルマーの最終定理」に由来する数論的代数幾何学の古典的難問を、位相数学の画期的方法で解決したことで世界的数学者の地歩を固めた。著書に『教養としての数学』『素数ファンタジー』『お父さんの数学旅行』『数学者たち』などがある。

----------

（数学者 キム・ミニョン）