ノーベル賞の数学理論の結論…｢理想の結婚相手｣に最短で出会うためにやるべきこと

※写真はイメージです - 写真＝iStock.com／kyonntra

理想の結婚相手を見つけるにはどうすればよいか。1962年に2人の数学者が発表した論文では、アルゴリズムを使い安定的な結婚相手とマッチングするための方法が紹介されている。後にノーベル経済学賞を受賞したその理論について、元オックスフォード大学教授のキム・ミニョンさんが解説する――。

※本稿は、キム・ミニョン『教養としての数学　数学がわからない僕と数学者の対話』（プレジデント社）の一部を再編集したものです。

■数学的思考で「結婚の成功」を考えてみる

世俗的な質問から話を始めましょう。「結婚仲介業を成功させるにはどうすればいいのか？」。

これがいまの私の関心事です。どう思いますか？　結婚の仲介をするとき、どんな要素が重要でしょうか？　お見合い相手の教育水準、家柄、文化、このようなことがうまくマッチしなくてはなりません。いずれも重要な要素です。行き届いた理論を組み立てるには、社会的・文化的な要素を熟考する必要があります。

ですが、いまはとりあえず単純な仲介問題、「選好度」だけにポイントを絞ったマッチング問題を考えましょう。

■男女2人ずつでのマッチングを考える

誰が誰を好きになるかということ以外に考慮すべきことがなければ、ただ好きな人同士をマッチングさせればいい、と考えることもできますね。つねにそのように簡単な例から探求が始まります。

投票問題と同じように、基本的な情報は選好度表にまとめればいいでしょう。男性は女性たちを、女性は男性たちを選好度の順に並べて、仲人である私たちに提出させます。最も単純な、男女が各2人という状況であれば4通りの選好度表ができます。

『教養としての数学』より

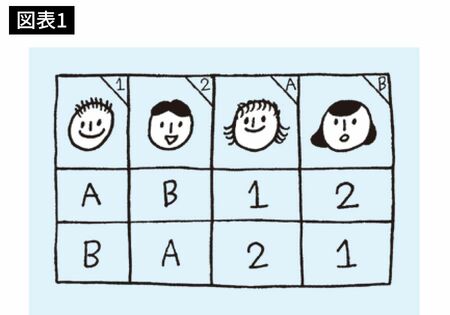
表の読み方はわかりますか？

男性1は女性Bより女性Aの方が好きであり、男性2は女性Aより女性Bの方が好き。このように読みます。では、どうマッチングすればいいでしょうか？

このケースはシンプルです。{男性1、女性A｝{男性2、女性B｝。このようにマッチングさせればいいでしょう。先に言ったように、ただ好きな相手同士をマッチングさせればいいと思います。

■功利主義では「よいマッチング」を考えることはできない

ところが問題は、現実にはこんな単純な選好度表はめったにできないという点です。普通はどんな現象が起こりますか？　図表2のようなケースの方が多そうです。

『教養としての数学』より

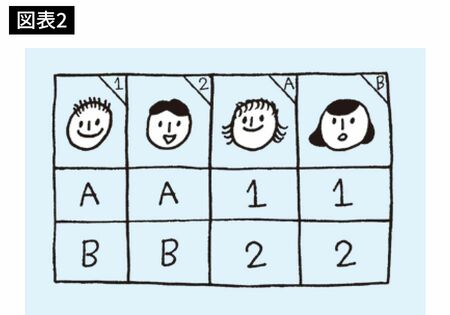
これはモテる男性とモテる女性がいる状況です。男女が2人ずつしかいなくても、こうしたケースはよくあります。今度はどうすればいいでしょうか？

可能性は2つしかありません。｛男性1、女性A｝{男性2、女性B｝とするか、｛男性1、女性B｝｛男性2、女性A｝とするかのどちらかです。

では、この2種類のうち、どちらの方がよいマッチングでしょうか？

もっと情報がないとわからないと思いますが、情報はこれだけとしましょう。

まず、｛1、B｝｛2、A｝について考えてみましょう。そうすれば各カップルに1人ずつは幸せになれますから。功利主義的な観点が示されましたね。

ですが、不幸にも功利主義では問題は解決しません。なぜなら｛1、A｝｛2、B｝としても幸せな人は2人、｛1、B｝｛2、A｝としても幸せな人は2人になりますから。満足する個人の数から見ても、2つの方法は同等に思われます。

でも、満足するカップルが多いことを基準にすれば、最初の場合の方がよりよい方法です。満足するカップルが生まれることがより重要だということ。それは非常に重要な指摘です。そのアイディアを足掛かりに、もう少し体系的に考えてみましょう。

■「モテる者同士で勝手にやってろ」

忘れやすい第一の仮定は、私たちが誰の立場にあるかということです。

私たちは結婚仲介業者の立場ですよね。そこが大事な点です。

第二の仮定は、はっきり言っていなかったかもしれません。ここでは、男性2人と女性2人が「必ず」この中でカップルをつくらなければならないということです。

もちろん現実と比べれば単純なシナリオですが、この手の数学的モデルは、より複雑な現実の状況に影響を及ぼすこともあります。この2つの仮定に留意しながら、再び問題を考えてみましょう。

1つヒントを出すと、結婚仲介業者のいない自然状態であれば、普通｛男性1、女性A｝｛男性2、女性B｝となりそうですよね？　すると「モテる者同士で勝手にやってろ」と気分を害する人もいるでしょうが、自然状態ではよくあるケースだと言えるでしょう。

事実、結婚仲介業者にとって重要なのは、自然なマッチングなのです。

その理由を考えるために、逆の状況を見てみましょう。

■結婚仲介業者が選ぶべきカップルの最適解

もし｛1、B｝｛2、A｝というカップルをつくったら、どんな現象が起きるでしょうか。

選好度に背いてマッチングすると、2組とも離婚する可能性が高くなります。いまの相手が嫌になった男性1と女性Aが、お互いを求めて浮気するかもしれません。

では、｛1、A｝｛2、B｝という組み合わせにしたら、男性2と女性Bはお互いを嫌いにならないでしょうか？　男性2が女性Aを好きでも、Aが自分のことを好きではないので、浮気のチャンスはありません。女性Bが男性1と付き合いたくても同様です。なので、いまの相手といっしょにいるしかありません。

このように、結婚仲介業者の立場からすると、多くのカップルが成立することが重要です。自分が仲介したカップルが破局に至るのは、ビジネスに悪影響を及ぼすでしょう。

ということは、私たち結婚仲介業者の立場からすると、｛男性1、女性A｝｛男性2、女性B｝とするのが正解です。この論理は、私たちの単純な仮定以外に何の情報も必要ありません。

ごく単純なケースを見てきましたが、男女が2人ずつしかいなくても、すでに何か数学的思考が必要になるような気がしますね。

3人ずつではどうでしょうか。講義でこの問題を出すと、学生をはじめ参加者全員が「わっ」と声を上げて頭を抱えます。難しいというのは予想できますよね？

ちょっと想像するだけで、この条件を満たすマッチングの場合の数がかなり増えるからです。3組、4組と増えるだけでも複雑そうなのに、ペアの数が26組にもなったらどうしますか？　非常に複雑に見えますね。

■カップルを“効率的に”生み出す仕掛けを考える

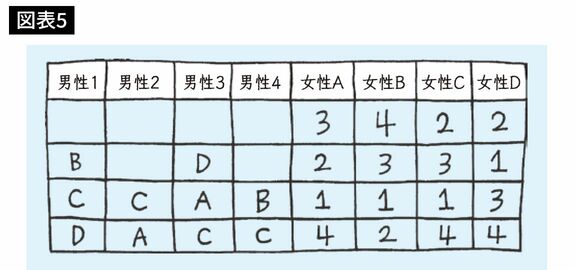
男女4人ずつのマッチングの例を示します。

ただ、先ほどとは違って、問題をもう少し論理的に解決するため、手続きと方法と規則を整理しながら考えていきます。一種のアルゴリズムをつくるわけです。

第1ラウンドでは、男性がいちばん好きな女性にプロポーズをします。

男性が好きな女性にプロポーズしたら、次の段階は何でしょうか？　女性にも選好度が与えられるべきです。男性の選好度が1人の女性に集中することもありえます。

そこで、女性は自分の選好度にしたがい、男性のプロポーズを受け入れるか断るかします。いちばん気に入った男性を選ぶわけです。

ただ、すぐに結婚するわけではありません。まず婚約をします。

ビクトリア朝のイギリスを舞台にした恋愛小説を思い浮かべればいいでしょう。ヨーロッパの古典的な慣例にしたがい、私たちのアルゴリズムでは、いま言ったように女性から婚約を破棄することができます。ですが、男性は一度婚約したら自分から破棄することはできません。では、例を見てみましょう。

『教養としての数学』より

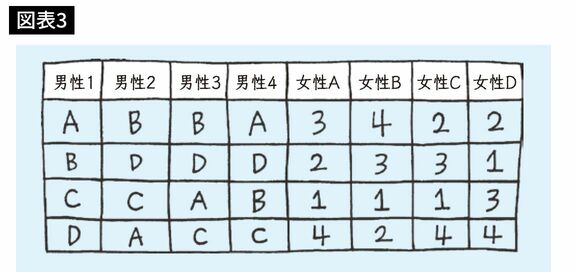
第1ラウンドでは、男性1と男性4は女性Aに、男性2と男性3は女性Bに、それぞれプロポーズします。選好度表を見ると、女性Aは男性1の方が好きで、女性Bは男性3の方が好きですから、｛1、A｝｛3、B｝の2組のカップルができます。そうすると、男性2 と4、女性CとDが婚約していない状態で残ります。

第2ラウンドでは、まだ婚約していない男性2と4が、第2順位の女性にプロポーズします。すでに行われたプロポーズを消してみましょう。

『教養としての数学』より

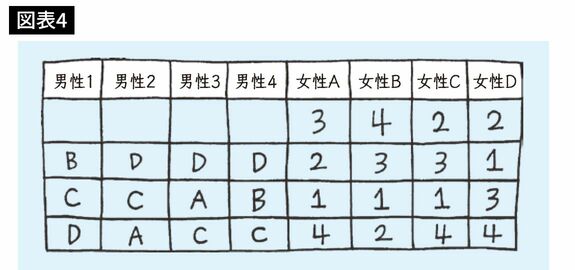
次は男性2と4が女性Dに同時にプロポーズします。するとここで、｛2、D｝というカップルができます。したがって、現在成立しているカップルは｛1、A｝｛2、D｝｛3、B｝の3 組になりますね。

■実生活と同様に「結婚後の安定性」を考慮する

実生活において、婚約はしばらく相手を観察する期間となります。結婚しても大丈夫かどうかを見守るわけです。婚約期間の観察中に、相手が結婚に合わないと思ったら、婚約を破棄することもありえます。

このゲームでは、まだすべてのラウンドが終わっていません。なぜでしょうか？

それは、「とりあえず婚約したとしても、結婚した後の安定性を考慮する必要があるから」です。それに、プロポーズを断られた男性もいるし、まだプロポーズを受けていない女性もいますから。

ここで問題になるのは男性4です。

■魅力的な女性1人を2人の男性が奪い合うと、どうなるか

第3ラウンドで男性4は選好度3位の女性Bにプロポーズする番です。

『教養としての数学』より

では、どんなことが起きるでしょうか？　それこそ恋愛小説のような構図ですね。

女性Bはすでに第1ラウンドで男性3と婚約していますが、もともとの選好度1位は男性4でした。婚約を破棄してもいいなら、女性Bは男性3との婚約を破棄して、もっと好きな男性4のプロポーズを受け入れるでしょう。

そうなると、男性3は再びラウンドに出て、選好度2位の女性Dにプロポーズすることになりますね。では、どんな問題が起きるでしょうか？

女性Dは、男性3よりも現在の婚約相手である男性2の方が好きですから、男性3からのプロポーズを断るでしょう。すると次にはこんな状況が起こります。

男性3は選好度3位の女性Aにプロポーズします。女性Aは現在の婚約者の男性1より男性3の方が好きなので、男性1との婚約を破棄して、男性3と婚約することになります。

ラウンド4が終わった段階で、成立しているカップルは｛2、D｝｛3、A｝｛4、B｝となります。そうすると、男性1がまたプロポーズをしなくてはなりません。

第1ラウンドで婚約した女性Aを男性3に奪われた男性1は、今度は選好度2位の女性Bにプロポーズします。ですが、女性Bは現在の婚約者の男性4と男性1を比べて、選好度が上位にある婚約者4との婚約を維持することを選びます。

挫折した男性1は、今度は女性Cにプロポーズします。いま相手のいない女性Cは、男性1のプロポーズを受け入れることになります。

最終的な組み合わせは｛1、C｝｛2、D｝｛3、A｝｛4、B｝となります。こうしてアルゴリズムは完結します。あとは結婚するだけです。選好度表をあらためて見直しながら、浮気する可能性を調べてみるとどうなるでしょうか。

たとえば、男性1はいまの相手より女性A、Bの方が好きですが、女性Aは自分の選好度1位の男性3と結ばれており、女性Bも第1位の男性4と婚約しているので、2人とも男性1 を受け入れる必要がありません。したがって、男性1にはもはやチャンスはありません。

■完璧に見えるアルゴリズムだが…

私たちが本当に結婚仲介業者で、男女のお互いの選好度情報を持っていれば、互いにお見合いをさせて時間を浪費する必要もありません。単にこのアルゴリズムのとおりにカップルをつくればいいだけだからです。

このアルゴリズムを作ったのは、デビッド・ゲールとロイド・シャプレーという二人の数学者です。1962年に発表した論文「大学入学と結婚の安定性」で紹介しています。

二人の名を取ってつけられた「ゲール＝シャプレー・アルゴリズム」は、答えがあるというだけでなく、答えを効率的に求める方法まで提示しています。これを使えば、男女の役割を取り換えることもできるし、答えが複数あればその中からどれを選択するかも考えることができます。シャプレーはこの理論によって2012年にノーベル経済学賞を受賞しました。

ただ、1つ疑問が浮かびます。

ゲール＝シャプレー・アルゴリズムでは、プロポーズできるのは男性だけとなっています。女性が先に選択できないのは、何となく女性に不利に思えますが、はたしてこのアルゴリズムは女性と男性、どちらに有利なんでしょうか？

■女性は「最も嫌いな男性」とマッチする

私たちが使ったアルゴリズムは、確実に男性にとって有利です。

図に示す例で少し調べてみましょう。

『教養としての数学』より

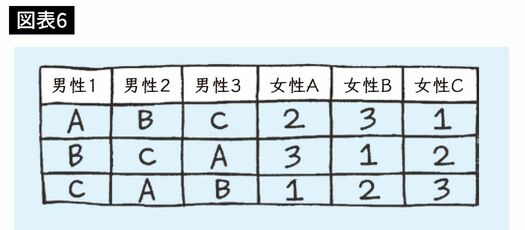
この表のようなケースをゲール＝シャプレー・アルゴリズムで考えてみると、第1ラウンドで男性1は女性Aに、男性2は女性Bに、男性3は女性Cにプロポーズしますね？　その次に、アルゴリズムはどうなりますか？

女性は自分にプロポーズした人の中から気に入った相手を受け入れます。ところが、女性がそれぞれプロポーズを1回しか受けられないので、第1ラウンドで男性1と女性A、男性2と女性B、男性3と女性Cがそれぞれ婚約することになります。

次の段階は第1ラウンドで選ばれず婚約していない男女が第2ラウンドでマッチングすることになりますが、第2ラウンドは行われずに終わります。｛1、A｝｛2、B｝｛3、C｝というカップルが成立して、結婚することになりますから。

このように見ると、女性たちは自分が最も嫌いな男性がプロポーズしてきても、このアルゴリズムにしたがってそのまま結婚しなくてはなりません。

一方、男性たちは自分がいちばん好きな女性と結婚することになります。男性たちが全員満足したため、他の女性を探す必要がないというわけですね。安定したマッチングではありますが……。

■アルゴリズムの教訓は「好きなら先に告白せよ」

ゲール＝シャプレー・アルゴリズムにおいて男性は自分にとってマッチング可能な女性のうち、選好度が最も高い女性と結婚することになります。

キム・ミニョン『教養としての数学　数学がわからない僕と数学者の対話』（プレジデント社）

そして、最終的に結ばれた女性よりも選好度が高い女性と結ばれようとすると、どこかに不安定性が生じます。

一方、女性はマッチング可能な男性のうち最も選好度が低い男性と結婚することになります。この現象を上の例がよく示しています。

こうして見ると、男性に圧倒的に有利な仕組みと言っていいでしょう。

私はある講義で、このアルゴリズムの教訓は「好きなら先に告白せよ」ということだと言いました。

もし振られたとしても、自分の選好度の順に告白する方がよい結果が得られるのですからね。男性の場合を考えると、選好度の低い女性とカップルになったとしても、すでにそれより選好度の高い女性からは振られた状態ですから、婚約破棄の原因はなくなっているわけです。

----------

キム・ミニョン 数学者
ソウル大学数学科を卒業し、イェール大学で博士号を取得。マサチューセッツ工科大学研究員、ユニバーシティ・カレッジ・ロンドン（ロンドン大学）教授などを経て、韓国の浦項工科大学（ポステック）教授、ソウル大学客員教授を歴任。2011年に韓国人数学者としてはじめてオックスフォード大学正教授に任用される。「フェルマーの最終定理」に由来する数論的代数幾何学の古典的難問を、位相数学の画期的方法で解決したことで世界的数学者の地歩を固めた。著書に『教養としての数学』『素数ファンタジー』『お父さんの数学旅行』『数学者たち』などがある。

----------

（数学者 キム・ミニョン）