｢100年に1人の天才｣でも｢最新のAI｣でも解けない…使うのは＋×÷だけなのに世界中の数学者が敗北した難問

※写真はイメージです - 写真＝iStock.com／Imgorthand

小学生でも理解できる内容なのに、世界中の数学者たちを悩ませる問題があるのをご存じだろうか。NHKの知的エンターテインメント番組「笑わない数学」の放送内容を再構成した書籍より、「コラッツ予想」についての箇所を紹介する――。

※本稿は、NHK「笑わない数学」制作班編『笑わない数学2』（KADOKAWA）の一部を再編集したものです。

■賞金1億2000万円の「見た目が単純すぎる未解決問題」

好きな数を一つ思い浮かべてください。ただし、分数や小数、マイナスの数ではなく、1、2、3などの自然数でお願いします。その数に次の操作をし、その計算結果にさらにこの操作をし、……のようにどんどん繰り返してみてください。

1　偶数なら2で割る
2　奇数なら3倍して1を足す

この操作を十分な回数繰り返すと「1」になりましたね？　1にならなかった方はどこかで計算ミスをしている可能性が高いです。

「計算ミスをしている可能性が高い」と書きましたが、本当に必ず1になるかどうか、実はまだ証明されていない数学の未解決問題なのです。この問題は「コラッツ予想」と呼ばれています。まるで数遊びのような見た目をしたこの問題は、次の予想が正しいかどうかを証明する問題です。

コラッツ予想
すべての自然数は、
1　偶数なら2で割る
2　奇数なら3倍して1を足す
という操作を繰り返すと、必ず1になる。

問題の内容は小学生にもわかるのに、80年以上もの間、世界中の数学者の挑戦をはねのけ続けている超難問です。なんと、1億2千万円の懸賞金までかかっているのです。

■ほんとうに1になるのか

この問題について考える前に、本当に1になるのかどうか、小さい数で試してみましょう。

まずは2から。2は偶数ですから、2で割って、1です。

3はどうでしょうか。3は奇数なので、3倍して1を足します。すると10になります。10は偶数なので、2で割ります。すると5。これは奇数なので3倍して1を足して、16。これは偶数なので2で割ると8、さらに2で割ると4、さらに2で割って2、さらに2で割って1になります。

では、少し大きな数にもチャレンジしてみましょう。例えば、129は次のように変化します。

『笑わない数学2』より

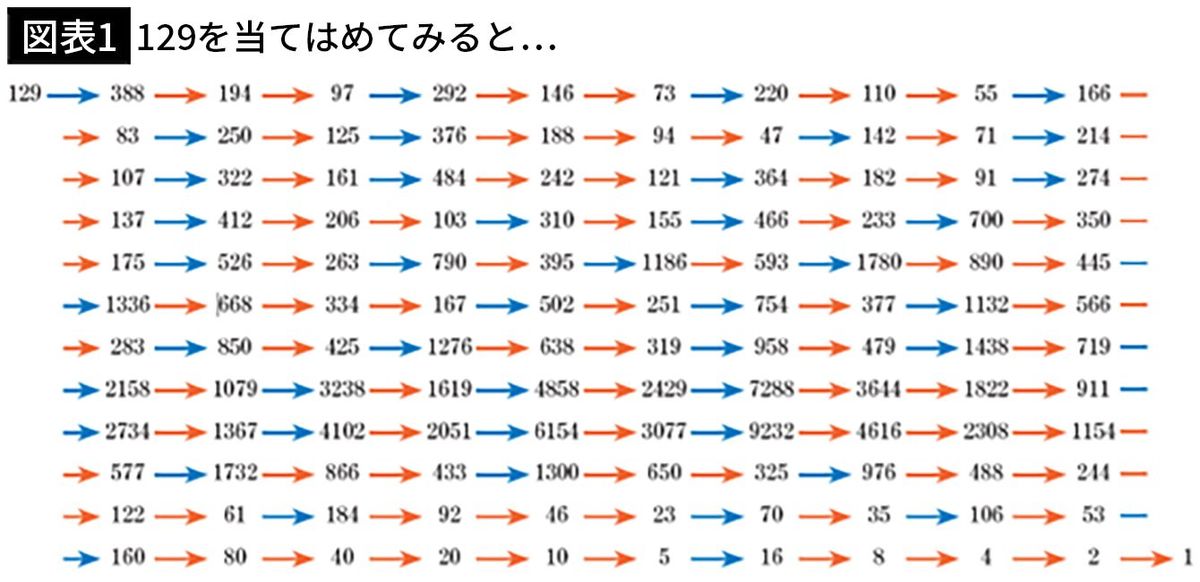
グラフにするとこんな感じ。

『笑わない数学2』より

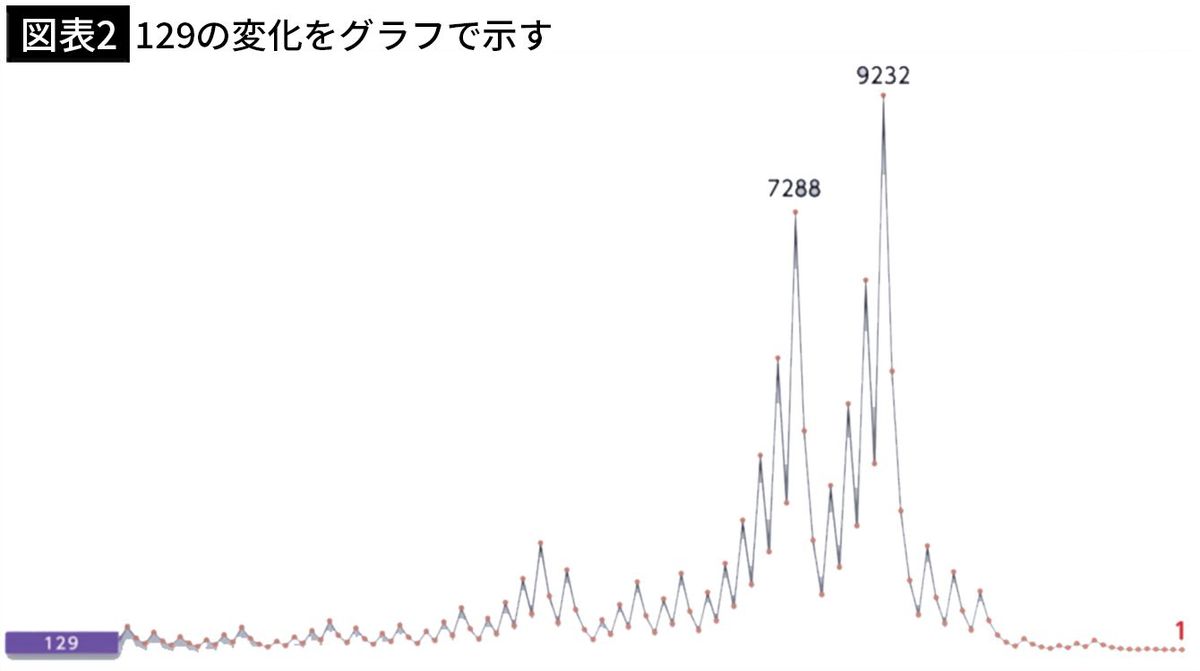
121回の操作で1になります。その間に9232まで値が大きくなっていますが、なんとか1になっています。これだけ大きい値になっても最終的にはちゃんと1になりましたね。

では、どんな自然数でも、最終的には1になるのでしょうか？

現在では、コンピュータを使ってものすごく大きな数まで1になることが確かめられています。最新の研究の一つによると、17垓7088京7431兆761億1695万5136以下の自然数はすべて、1になることがわかっています。

ここまで確かめたのなら、もうコラッツ予想は正しい！　と言いたいのですが……残念ながら、これよりも大きな自然数は無限にあります。ですから、ここまで確かめても、コラッツ予想が正しいとは言い切れないのです。

つまり、コラッツ予想を証明するには、なんらかの方法で、無限個の自然数が1になることを一気に示す必要があるのです。

■きっかけは学会の休憩時間での雑談

ここでちょっと、コラッツ予想の歴史を紹介しましょう。

「コラッツ予想」という名前ですから、当然、数学者のコラッツさんが生みの親です。その名は、ドイツの数学者ローター・コラッツ。

ただし、実はコラッツ自身は、コラッツ予想について正式な研究成果は残していません。したがって、論文も一本もありません。彼のコラッツ予想に関する発表といえば、80年代に自分の思い出話をつづったエッセイくらいしかないようです。

では、どうやってコラッツ予想は広まったのでしょうか。

広まるきっかけとなったのは、1950年、アメリカで開かれた数学の学会。そこで、コラッツがこの予想を発表……したわけではなく、学会の休憩時間に他の数学者に世間話のように話し、そこから広まったと言われています。

当時、それを聞かされた数学者たちの反応はどうだったのか？　残念ながら記録が残っていないのでわかりませんが、おそらく、そこまで難解な問題だとは、誰も思わなかったのではないでしょうか。

見た目は小学生でもわかるほど簡単な問題。高度な計算力もいりませんから、つい解きたくなってしまいます。しかしその一方で、どこから手を付ければ良いかがわからない不思議な問題として、じわじわと世界に広まっていくことになりました。

ドイツの数学者ローター・コラッツ（写真＝Jacobs, Konrad／CC-BY-SA-2.0-DE／Wikimedia Commons）

■「人生を棒に振りかねない危険な難問」

数々の有名数学者がコラッツ予想に挑みました。例えば、スタニスワフ・ウラム。東西冷戦の最中、アメリカで核兵器の開発に取り組んでいましたが、コラッツ予想に夢中になってしまいます。しかし、何の結論も導くことができませんでした。

アメリカでは「コラッツ予想は、アメリカの研究を遅らせるための陰謀ではないか」というジョークが生まれるほどでした。

やがて数学者たちは「のめり込むと人生を棒に振りかねない危険な難問だ」として、この問題を敬遠するようになりました。そして今では多くの数学者が「敗北宣言」を出すほどの超難問として恐れられています。

では、この超難問「コラッツ予想」は手つかずのまま放置されているのでしょうか。いえ、そうではありません。それでもなお諦めない数学者たちがある種の「妥協」を行うことで、コラッツ予想の牙城を切り崩そうとしました。

■証明の第一歩はまさかの「妥協」

1970年代、2人の数学者リホ・テラスとコーネリアス・エベレットがそれぞれ独立に、それまでとは異なるアプローチを取り始めました。

NHK「笑わない数学」制作班編『笑わない数学2』（KADOKAWA）

コラッツ予想は、例の操作を繰り返すと「すべての数」が「やがて1になる」という予想でした。そこでエベレットたちは、「すべての数」についての証明をいったん忘れ、「ほとんどすべての数」についての証明を目指すという「妥協」を行うことにしたのです。

少し難しくなりますが、2人はすべての数から一部の数を確率的に取り除き、その残りの数について、コラッツ予想を証明しようとしたのです。

では、この方法で、2人は証明に近づけたのでしょうか？

実は、2人はさらにもう一段階、「妥協」することになりました。

それは「やがて1になる」こともいったん忘れ、「自分自身より小さくなる」ことを証明するという「妥協」でした。

つまり2人は、次の定理を証明したのです。

ほとんどすべての自然数は、コラッツ予想の操作を繰り返すことで、
自分自身より小さくなる

このことは、まだ1に行くとわかっていない数、例えば100垓くらいの数について、操作を繰り返すと、いつかは自分自身よりも小さくなることが示された、ということを意味します。

こんな妥協した証明に意味はあるのか？　と思われる方がいるかと思います。彼らの妥協は賢明な決断で、大きな進歩につながったのです。

■数学者たちの惨敗宣言

彼らの論文発表からまもなく、フランスの数学者ジャン・ポール・アリューシュがもう一歩前進します。

アリューシュは1979年、次の結論にたどり着きました。

ほとんどすべての数は、コラッツ予想の操作を繰り返すと、
自分自身の約0.869乗よりも小さくなる

これはつまり、100垓くらいの数なら、いつかは1300京よりも小さくなることを示した、ということです。

そしてさらに15年後の1994年、スロバキアの数学者イバン・コレックが次の結論にたどり着きました。

ほとんどすべての数は、コラッツ予想の操作を繰り返すと、
自分自身の約0.7925乗よりも小さくなる

これは、100垓くらいの数が、いつかは27京よりも小さくなることを示した、ということになります。

「妥協」を重ね、コラッツ予想に挑み続けた数学者たち。しかし結局のところ、コラッツ予想の完全な証明にはまったくたどり着いていないと言わざるを得ません。そのため、数学者たちのほとんどは、「もう証明に挑むのは止めよう」と思うようになっていきました。

そんなときでした。コラッツ予想にものすごく近付いたと言われる証明が、ついに現れたのです。それは2019年のことでした。

■数学界のスーパースターが挑んだ結果は…

証明を書いた人物は、9歳でオーストラリアの大学で学び、17歳でアメリカのプリンストン大学の大学院に入学、31歳で数学界の最高栄誉とされるフィールズ賞を受賞し、天才の名をほしいままにしてきた数学界のスーパースター。その名も、テレンス・タオ！

タオは次の結論にたどり着きました。

ほとんどすべての自然数は、コラッツ予想の操作を繰り返すことで、
ある意味好きなだけ小さくなる

まさに、コラッツ予想の証明に限りなく肉薄したのです！

1985年、アデレード大学でテレンス・タオを教えるポール・エルデシュ（写真＝Billy or Grace Tao／CC-BY-SA-2.0／Wikimedia Commons）

しかしタオ自身は、自分の証明についてこのように述べています。

「私たちはコラッツ予想に好きなだけ肉薄できるようになりました。しかし、実際のところは、完全な証明にはまったく手は届いていません。」

タオの証明も、すべての数から一部の数を取り除いているため、完全な証明には程遠いのです。

もしかしたら、コラッツ予想の証明には、まったく新しい数学が必要になるのかもしれません。

コラッツ予想は、一人の数学者の、いわば思い付きから始まった、とっておきの数字遊びです。小学生にも理解できる内容でありながら、その証明は、現代数学をもってしても歯が立ちません。

果たして、コラッツ予想の証明には、まったく新しい数学が必要なのでしょうか？

それとも、誰も気づいていないだけで、既存の手法で解ける問題なのでしょうか？

はたまた、実は間違った予想なのでしょうか？

その答えはまだ、誰も知りません。

----------

NHK「笑わない数学」制作班 パンサー尾形貴弘が難解な数学の世界を大真面目に解説する異色の知的エンターテインメント番組。レギュラー番組としてNHK総合テレビで、シーズン1が2022年7月から9月まで、シーズン2が2023年10月から12月まで放送された。シーズン1はギャラクシー賞テレビ部門の2022年9月度月間賞に選ばれた。過去の番組はNHKオンデマンドやDVDで確認することができる。

----------

（NHK「笑わない数学」制作班）