｢1/2と1/3どちらが大きい?｣わからない小5が5割以上いる…東大教授が｢さすがにまずい｣と心配するワケ

※写真はイメージです - 写真＝iStock.com／imtmphoto

「1／2と1／3のどちらが大きいか」という問いに対して、分数を習いたての5年生の正答率が5割を切っていたという調査結果があります。東大教授の西成活裕さんは「答えがわからない子は、直感がはたらいていないのかもしれません。算数・数学の世界では論理的思考だけではなく直感やイメージも非常に重要です」といいます。奥深い「算数」の世界について、文系ライターの郷和貴氏との会話形式でお届けします――。

※本稿は、西成活裕『東大の先生！文系の私に超わかりやすく算数を教えてください！』（かんき出版）の一部を再編集したものです。

■算数で大切なのは直感力と論理的思考力

【郷さん】先生は以前、「数学を勉強する目的は論理的思考力を養うこと」っておっしゃっていましたけど、それは算数でも同じですか？

【西成先生】うっ！

【郷さん】どうしたんですか？　変な汗がでてますよ。

【西成先生】テレビの全国放送でもそういっちゃったんですけど、この場を借りて発言を訂正します。

【郷さん】○コちゃんに怒られますよ（笑）。

【西成先生】いや、最近ね、数学で大事なのは論理的思考力だけじゃなくて、直感力も大切だなとつくづく思うんですよ。

【郷さん】直感力？

【西成先生】はい。「イメージ」や「感覚」といってもいいです。論理が大切である事実は1ミリも揺るがないんですけど、同じくらい直感も大事だと考えるようになりました。先日亡くなった、ノーベル経済学賞を受賞したダニエル・カーネマン博士の「システム1」「システム2」という思考回路のモデルはご存じですか？

【郷さん】ああ、「プロスペクト理論」でしたっけ。ひと昔前のビジネス書によく書いてありました。

【西成先生】そうそう。「直感」や「イメージ」で瞬時に結論を出せるのがシステム1の「速い思考」。「論理的」にじっくり考えて結論を出せるのがシステム2の「遅い思考」。「人はこの2つの思考回路を使い分けていて、必ずしも合理的な判断をしているわけじゃない」と博士はいったわけです。

【郷さん】ふんふん。

【西成先生】で、私がいままで「数学を学ぶ目的」として主張してきたのが、「論理的思考力（システム2）を鍛えること」だったんですよ。なぜなら数学の問題を解いているときってふだんの脳の動きとは異なり、システム2にめちゃくちゃ負荷がかかるからです。その経験を子どものときから何度もしていると、数学に限らず、なにか物事を考えるときに感情に引きずられたりしないで、筋道立てて考えることが得意になる。そのメリットは大きいよね、という話をしてきたんです。

【郷さん】……いままでは。歯切れが悪いですね。

■1／2と1／3どちらが大きい？

【西成先生】実は、数学の世界って論理的思考だけじゃなくて、直感やイメージもめちゃくちゃ大事だったんです。先日、衝撃的なデータを知ったんです。慶應義塾大学の今井むつみ教授が広島県の小学校で行った調査によると、「1／2と1／3のどちらが大きいか」という問いに対して、5年生の正答率が5割を切っていたそうです。

【郷さん】え！　小学5年生なら分数を習いたてじゃないですか。

【西成先生】肝心の分数の「意味」を理解できていないんです。大きさの比較なら、たとえば1／2と1／3の大きさのピザをイメージできたら答えられるはず。それができていないのはさすがにまずいです。直感がはたらいていないんじゃないか、と。

【郷さん】たしかに、衝撃的なことかも……。でも、なんでそんなに直感が大事なんですか？

【西成先生】そもそも論理的思考だけだと、数学ってまったく進化していないはずなんです。たとえば、アイザック・ニュートンは運動の3法則や万有引力の法則を導きだすために「加速度（速度の変化の度合い）」という、それまで科学の世界で存在しなかったアイデアを思いつき、さらにそれを計算する手段として「微積分」という計算方法までつくりだしてしまいました。でもそれって、従来の数学や物理のロジックをいくら緻密に積み上げても、たどりつかないわけですよ。

【郷さん】「ひらめき」が必要になると。ビジネスの世界もそうですよね。

【西成先生】そう。あるいは「あれ？　なんか違くない？　こっちじゃない？」という動物的嗅覚みたいなものです。

■なぜ、算数で直感力を鍛えられるのか

【郷さん】ただ、いまの話って大学以上の数学に携わる人の話であって、私のような文系人間や、小学校の算数ではあまり関係ない気がしたんですが……。だって正しく計算できるようになることが算数の目的ですよね？

【西成先生】いや、算数でもイメージや直感って大事なんです。もちろん算数や数学の世界で論理が破綻すると計算ミスに直結しますから、論理的思考が大切なことは変わりません。システム2は絶対に必要だし、鍛えないといけません。ただ、そこにイメージや直感も織り交ぜていくと、算数や数学がより簡単に思えてくるんじゃないかなと思うんですよ。

【郷さん】具体的には？

【西成先生】先ほどいった「分数をみたときにピザが思い浮かぶ」もそうだし、図形問題なんて完全に「イメージできたもの勝ち」の世界なんです。どれだけ論理的思考が得意な子でも、目の前にある三角形を頭の中でクルンと回転させたり、裏返したりできないとなかなか解けません。あるいは計算問題で「2933＋4015」という問題があったとします。これ、論理的思考だけ使う子どもは、いきなり一の位から問題を解こうとしますよね。

【郷さん】そうでしょうね。

写真＝iStock.com／taka4332

※写真はイメージです - 写真＝iStock.com／taka4332

【西成先生】ここでイメージや直感を織り交ぜるとは、いきなり解こうとせずに、「ざっくりどれくらいの数になるかな？」って考えることなんですよ。「2933はほぼ3000。4015はほぼ4000。だから『2933＋4015』の答えは7000くらいだろう」ってざっくり計算する。そうするとたとえ計算ミスをして答えが「7948」になったとき、「あれ？　1000もずれるわけがないだろう。もう一度計算してみよう」って思えるはずです。

【郷さん】あ、それわかります。以前、娘に「15＋7」みたいな問題をさせたときに、じーっと考えた末に「12」って答えたんですよ。「なんで減ってんねーん！」ってツッコミたくなりましたけど。

【西成先生】いきなり正確な答えを出そうとして焦ったんでしょうね。「15に7を足したら20を超えそうだな」とまずはざっくりイメージをつかむ。細かい計算はそのあとでいいんです。この「まずはイメージをつかむ」解き方は、とくに算数が苦手な子どもたちにぜひ教えたいですね。

■3枚のピザを1／3で割ると何枚になる?

【西成先生】イメージや直感から入ったとしても、最終的には論理的思考を使わないと問題は解けません。図工だったら直感オンリーでもいいんですけど、算数や数学ではそうはいきません。すると、当初のイメージや直感とは異なる答えになることもあるんです。

たとえば「3枚の丸いピザを1／3で割ったら何枚か」という問題を見たとき、ひとり1枚ずつ食べているイメージが思い浮かぶ人もいるはずです。大人でも。

【郷さん】違うんですか？

【西成先生】ほらいた（笑）。「3で割る」のではなく、「1／3で割る」なので、論理的に考えてみると答えは「9枚」。「3枚の丸いピザのなかに、1／3の大きさのピザの切れ端は何枚ありますか？」という問いなので、答えは9枚です。

『東大の先生！文系の私に超わかりやすく算数を教えてください！』（かんき出版）P.33より

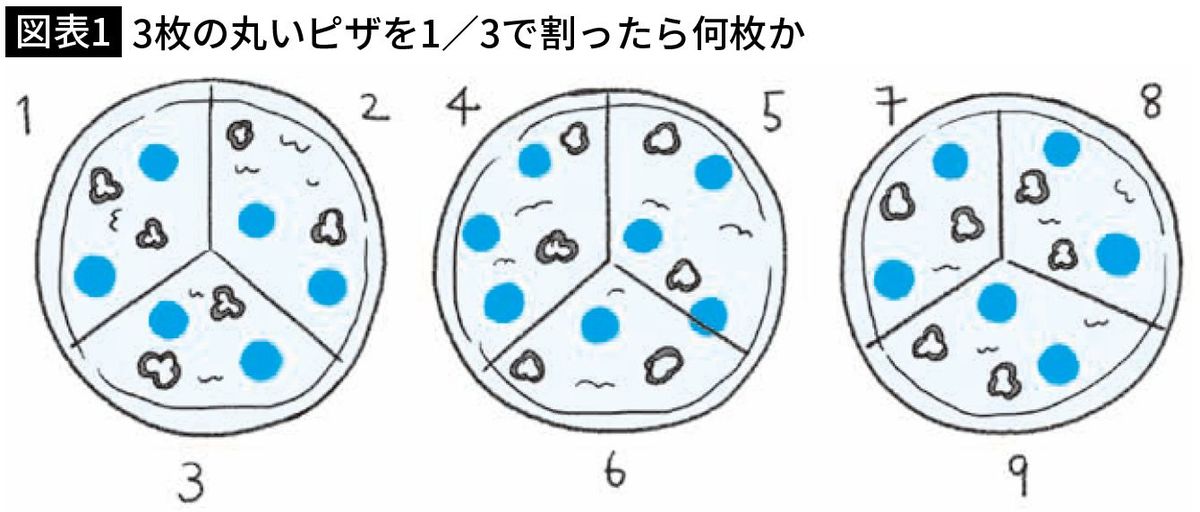
【郷さん】あっ、そっか。

【西成先生】いまみたいに直感と論理を切り替えながら算数や数学に取り組んでいくと、最初にパッと浮かぶイメージや直感が少しずつアップデートされていくんです。

【郷さん】AIでいう、学習データが増えて精度が上がるみたいな。

【西成先生】そう。あるいはビジネスの世界でいう「経験則」のことですね。「うちの社長、感覚的な意思決定しかしないし、ロジカルな話は苦手だけど、社長のいうことに従っていればなぜかうまくいくよね」みたいな世界です。

【郷さん】います、います、そういう人（笑）。

■直感と論理を行き来できる脳をつくるには

【西成先生】でしょ（笑）。そういう人って過去にいろんな成功体験と失敗体験をしていて、意識せずともちゃんと学習しているんですよ。だからいちいち論理的思考を使わなくても、それなりの精度で答えがでてしまう。私が提唱したいのは、システム1とシステム2をカチャカチャ切り替えながら、システム1自体の精度を上げていくことを「意識的に」行うことです。

写真＝iStock.com／bymuratdeniz

※写真はイメージです - 写真＝iStock.com／bymuratdeniz

【郷さん】どうやって？

【西成先生】イラストを使ったり、子どもたちに身近な例を使ったりして、できるだけ「意味」を理解してもらうように努めます。機械的に計算を解くだけが算数じゃないので、ちゃんと腹落ちさせたいんです。同時に、算数や数学の世界の面白さも伝えられたら理想かなと思っています。

西成活裕『東大の先生！文系の私に超わかりやすく算数を教えてください！』（かんき出版）

意識的に直感と論理を行き来する脳を鍛えることは算数や数学に限らず、大人になったときに絶対に役立つと思うんですよ。どっちかに偏っていてもそれは個性として別にいいんですけど、直感と論理を両方使える人ってこれからは希少価値が高いと思うんです。

【郷さん】たしかにAIがより身近な存在になりますからね。

【西成先生】そう、それもあるんです。論理的思考がめちゃくちゃ得意なAIが「自分のもうひとつの脳」として身近にある時代にすでに突入したことを考えると、イメージや直感はなおさら大切だと思うんです。

----------

西成 活裕（にしなり・かつひろ）
東京大学 先端科学技術研究センター教授
専門は数理物理学、渋滞学。東京大学工学部卒業、同大大学院工学系研究科航空宇宙工学専攻博士課程修了。その後、ドイツのケルン大学理論物理学研究所などを経て現在に至る。予備校講師のアルバイトをした経験から、わかりやすく教えることを得意としている。『東大の先生！ 文系の私に超わかりやすく数学を教えてください！』（かんき出版）は、20万部を超えるベストセラーに。

----------

（東京大学 先端科学技術研究センター教授 西成 活裕 イラスト＝meppelstatt）