｢運動が得意な子は勉強もできる｣は本当か…科学的思考ができる人なら分かる｢相関関係｣と｢因果関係｣

※写真はイメージです - 写真＝iStock.com／Radachynskyi

科学的思考を身に付けるにはどうすればいいか。サイエンスライターの竹内薫さんは「この世界は原因と結果の矢印がものすごいネットワークになっていて、非常に複雑なことが起きている。相関関係と因果関係のパターンをいくつか頭に入れておくといいだろう」という――。

※本稿は、竹内薫『フェイクニュース時代の科学リテラシー超入門』（ディスカヴァー・トゥエンティワン）の一部を再編集したものです。

■相関関係と因果関係を取り違えるリスク

科学リテラシーが問われるとき、「データをどう理解するか、読み解くか」は非常に重要な視点です。なかでも実社会でいちばん重要なのは「相関関係」と「因果関係」を理解すること。それなのに学校ではちょっとしか教えてくれなかったりするので、データを正しく読めない人が多いんです。

たとえば、図表1のグラフを見てください。要素Aの数と要素Bの数の増減に関連性があるという結果が出ています。つまり、AとBの相関関係があるとわかります。

出所＝『フェイクニュース時代の科学リテラシー超入門』（ディスカヴァー・トゥエンティワン）

間違えがちなのが、この相関関係を、因果関係と捉えてしまうこと。つまり、Aを原因としてBが起きた、あるいはBを原因としてAが起きたと関連づけてしまうんですね。グラフの横軸が原因で、縦軸が結果だと思い込んでいる人も多いです。でも、そんな決まりはどこにも書いてありません。

■警察官が増えると、犯罪率が上がる？

それに、相関関係はあるけれども単なる偶然で、何の因果関係もないのはよくあることです。有名なのが「地球が温暖化すると、海賊が減る」という相関関係。実際にグラフにしてみるとそういったデータが出てくるのですが、温暖化したから海賊が減ったという因果関係も、もちろん海賊が減ったから温暖化が進行するという因果関係もありません。

因果関係があっても、原因と結果を逆に捉えてしまう事例もあります。

たとえば「警察官の数が増えると、犯罪率が上がる」というもの。「警察官が増えて、取り締まりを無理やり強化したから犯罪率が上がる」と考える人もいます。確かにあり得ないとは言い切れないですが、これは因果関係を逆に考えたほうがよさそうです。犯罪率が上がったから、それに対応するために警察官の数を増やしたわけですね。

これだけ見ると笑い話のようですが、実は私たちの日常の中でも、このように因果の順番を捉え間違えていることは案外多いものです。

■「隠れた因果関係」に気付けるかどうか

あるいは、AとBの相関関係の裏に、別のCという原因が隠れていることもあります。

たとえば、「運動能力の高い子は勉強ができる」という相関関係。多くの人がこのデータを見ると、ついつい「運動能力の高さ」と「勉強ができる」ことの因果関係を読み取ろうとします。「運動能力が高いと脳が発達するから、勉強もできるのか」とか、「運動能力が高い子は勉強にも集中して取り組める」とかいろいろ考えるんですね。

でもおそらく、このデータの裏側にあるのは「親が教育熱心」という原因Cです。親が教育熱心だから子どもには良い環境を与えるし、勉強も運動もできる子になってほしいと考えて、どちらにもお金をかける。そうすると子どもの成績は良くなるし、運動もできるようになるわけです。

つまり、ここには隠れた因果関係があるんですね。運動能力と学校の成績に直接の因果関係はないけれど、共通の原因を持っていて、運動能力も学校の成績も、2つの結果が並んでいるにすぎないんです。

■「アイスのせいで犯罪が増える」という誤解

ほかにも、「アイスクリームの消費量が増えると犯罪が増える」という事例があります。これは「気温が上がる」が共通の原因です。気温が上がるとアイスを食べる人が増えるし、気温が上がると、外に出歩く人が増えてトラブルも増える。

さすがにアイスの消費量と、犯罪率は関係がなさそうだとわかりますよね。ただ、現実には因果関係を見誤って、「アイスのせいで犯罪が増えるからアイスをやめよう」なんておかしな判断をしてしまうこともありうるわけです。

こうした背景を見ていく分野を、因果推論と言います。最近は関連書籍も増えてきていて、いま非常に注目されている分野です。

因果関係については、有名な「モンティ・ホール問題」の事例がおもしろいので、紹介します。これはアメリカに実在したクイズ番組「レッツ・メイク・ア・ディール」の司会者、モンティ・ホール氏から名前をとっており、クイズ番組の内容を下敷きに考えられた問題です。

■あなたが開ける扉に新車はあるのか…

さて、あなたがそのクイズ番組の参加者だとしましょう。クイズに答えて勝ち抜いていくと、最後に景品がもらえます。ただ、その景品は3つの扉の奥に隠れています。当たりの扉は1つだけで、その扉を開けると、新車があります。ハズレの扉を開けると、ヤギが出てきます。「メエ～」と鳴いて、はい残念でした、というわけです。

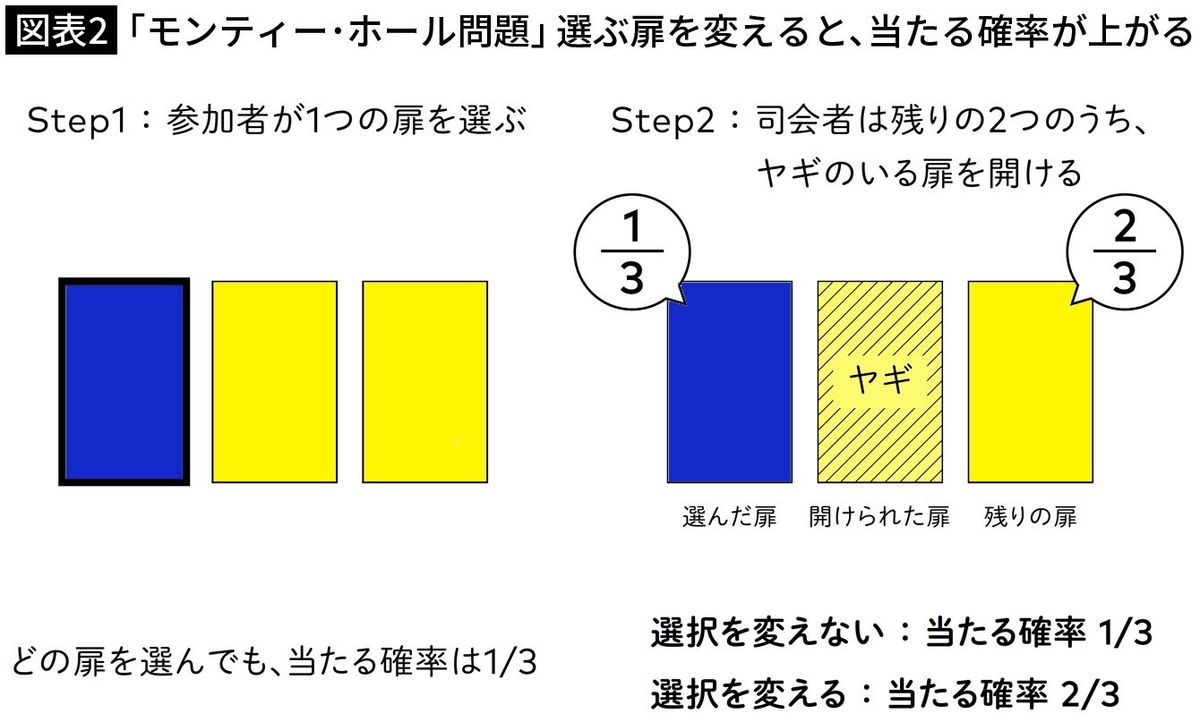
まず、クイズを勝ち抜いたあなたは、扉を1つ選びます。その後ろには新車があるかもしれないし、ヤギがいるかもしれない。まだ扉は開けないでおきます。ここでは、当たる確率は3分の1ですね。

おもしろいのが、そのあと司会者のモンティ・ホールさんが、あなたが選ばなかった残り2つの扉のうち、ヤギのいるほうを開けてくれるのです。まだ開けられていない扉は2つになりますね。そして、こう質問してきます。「最初に選んだ扉のままにしますか。それとも、選択を変えますか」。

実はここで、最初に選んだ扉をやめて、残りの扉に変更したほうが、当たる確率が上がります。不思議ですよね。最初に選んだ扉か、残り1つの扉か、どっちかを選ぶんだから確率は50％・50％、と普通は考えます。

■「モンティ・ホール問題」のカラクリ

なぜ当たる確率が変わるのか、解説しましょう。

最初に扉を選んだときの当たりの確率は3分の1。これはわかりますよね。ここで、選ばなかった2つの扉をまとめて袋に入れる、みたいなイメージをしてみてください。

この袋を選んだほうが、3分の2の確率で当たります。そして袋の中で、風か何かが吹いて扉が1つ開いちゃったと。それでもこの袋を選べば、確率は3分の2のままなんです。どうでしょう。イメージできますでしょうか。

出所＝『フェイクニュース時代の科学リテラシー超入門』（ディスカヴァー・トゥエンティワン）

もう少しわかりやすくするために、扉の数を仮に100としましょう。当たりは1つだけです。最初にランダムで選んだら、当たる確率は100分の1ですよね。そのあと、モンティ・ホールさんが残りの99の扉のうち、98個を開けてくれるんです。

その場合、最初に選んだ扉のままにするか、残る1つに変えるか、どちらが当たりそうですか。なんとなく、変えたほうが当たるように思えるのではないでしょうか。実際に計算すると、変えたほうが当たる確率は、100分の99です。

■2つの原因から1つの結果が生じる因果関係

これは、かなり因果関係が複雑なんですね。司会者がどの扉を開けるかに、制限がかかっています。残りの2つがハズレならどちらを開けてもいいけれど、どちらかに当たりがあるなら、そうじゃないほうを開けなければならない。つまり、司会者が扉を開けるという結果に対して、次の2つの原因が関係しているんです。

1つは、参加者が最初にどの扉を選ぶか。もう1つが、当たりがどこにあるのか。参加者が選んだ扉を司会者は開けることができないし、当たりの扉を開けることもできないわけです。この2つの原因があって、モンティ・ホールさんは1つの扉を開けるという結果が出ます。

先ほどの例にあった、「教育熱心な親」という1つの原因に対して、「運動ができる」「勉強ができる」という2つの結果が出ていたパターンとは、逆ですよね。今回のモンティ・ホール問題は、2つの原因から、1つの結果が生じている。この形の因果関係は、ぱっと考えてみても、なかなか理解が難しいです。

■人間の脳がスルーしてきた問題かもしれない

人間は、1つの原因が複数の結果を生んでいるパターンは比較的、見破ることができます。「今われわれが見ているのは結果だけだ、隠れた原因を探せ」というのは分析がしやすいんですね。原因の特定は比較的可能で、しかも早くできるので、人間は進化の過程で、見破る技を身につけてきたのでしょう。

一方で「今われわれが見ているものの原因はいったい何だろう。原因は1つではなく複数かもしれない」と考えると、非常に分析が難しい。

原因がたくさんある場合、人間にとって未知の原因もあり得ます。それがいったいいくつあるのかもわからないとなると、人間の脳はそれに対応するようにはできてこなかったんでしょうね。おそらく、複雑すぎるので無視したほうが早かったのかもしれません。

■「原因→結果」以外のパターンも覚えておこう

さてここまで相関関係、因果関係の話を詳しくお話ししてきました。相関関係の中にある因果関係のパターンをいくつか知っておくと、統計にだまされない頭を鍛えることができます。相関関係を見たら、その背後にあるかもしれない因果関係のネットワークをちょっと考えてみることです。

ここまで紹介した4つのパターンをまとめます。

出所＝『フェイクニュース時代の科学リテラシー超入門』（ディスカヴァー・トゥエンティワン）

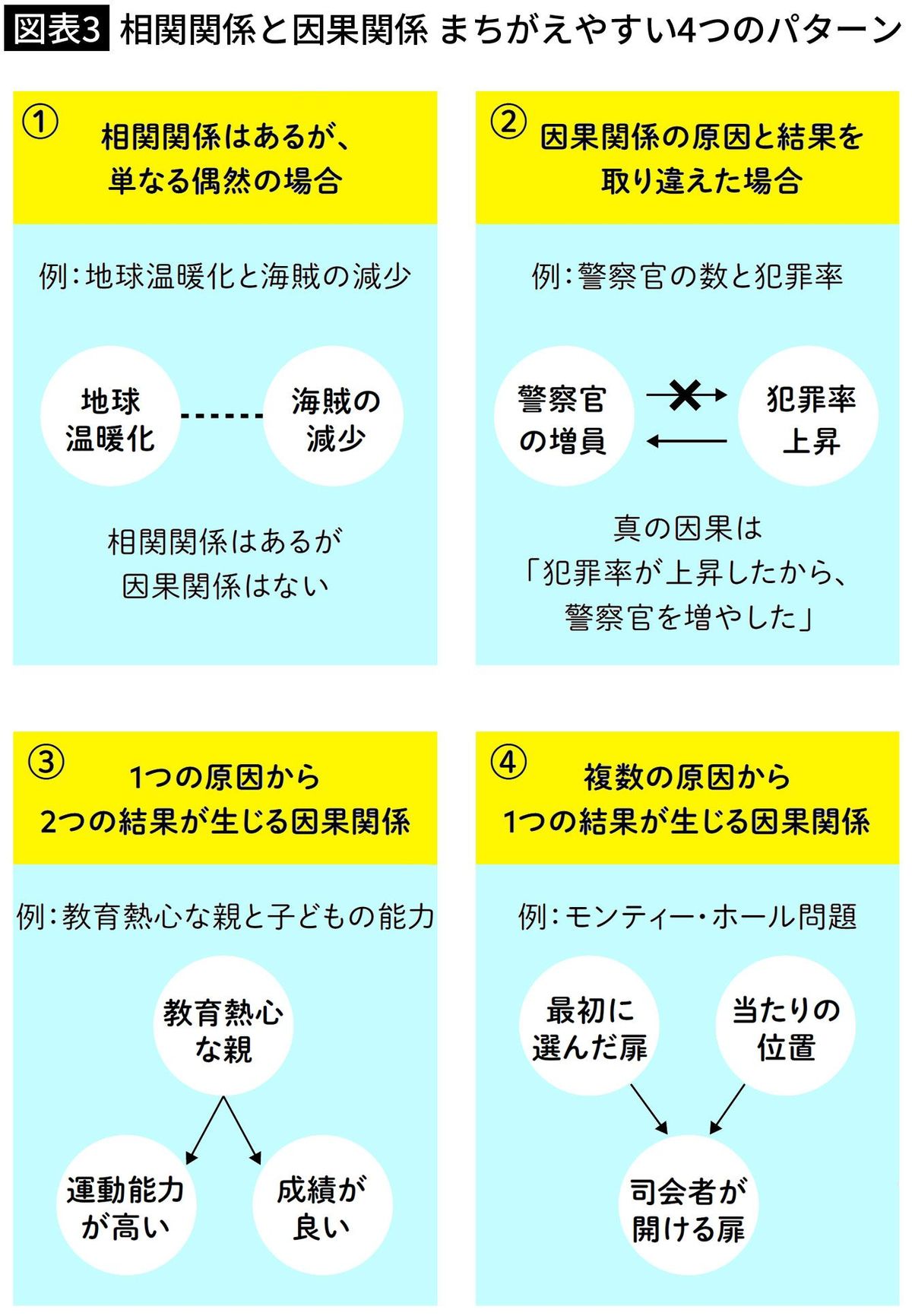
1つめは相関関係はあるけれど、単なる偶然の場合。海賊と地球温暖化の事例ですね。

2つめは、因果関係の原因と結果を取り違えるもの。警察官の数と犯罪率の事例を紹介しました。

竹内薫『フェイクニュース時代の科学リテラシー超入門』（ディスカヴァー・トゥエンティワン）

3つめが、1つの原因から2つの結果が生じる因果関係。教育熱心な親が原因で、学校の成績と運動能力という2つの結果が生じる事例と、気温が上がるという原因から、アイスの消費量が増え、犯罪数が増えるという2つの結果が生じる事例をお話ししました。

4つめが、モンティ・ホール問題のように、複数の原因から1つの結果が生じる因果関係です。

1つの原因から1つの結果が生まれるパターンしか頭の中にないと、怪しいデータを見破れません。それに私たちの生きる実際の世界は、原因と結果の矢印がものすごいネットワークになっていて、非常に複雑なことが起きています。なかなか自分で分析するのは難しいので、事例をたくさん知っておくといいでしょう。

----------

竹内 薫（たけうち・かおる）
サイエンスライター
1960年、東京都生まれ。東京大学教養学部教養学科（科学史・科学哲学専攻）、東京大学理学部物理学科卒業。マギル大学大学院博士課程修了（高エネルギー物理学理論専攻）。理学博士。大学院を修了後、サイエンスライターとして活動。物理学の解説書や科学評論を中心に100冊あまりの著作物を発刊。物理、数学、脳、宇宙など、幅広いジャンルで発信を続け、執筆だけでなく、テレビやラジオ、講演など精力的に活動している。

----------

（サイエンスライター 竹内 薫）