「マウスカーソルが最短時間で行ける領域はどれ？」──25年大学入試「情報I」の“不可解な問題”をLINEヤフーが考察

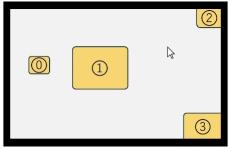
2025年大学入学共通テスト「情報I」第1問の問4aで出題された画面構成

　LINEヤフーに所属する山中祥太さんが発表した論文「実質的に無限大サイズを持つターゲットのポインティング： 2025 年大学入学共通テスト「情報 I」問題の一考察」は、2025年の大学入学共通テスト「情報I」において出題されたマウスカーソルでのターゲット選択に関する問題について、その妥当性を考察した研究報告である。

　問題は、画面上に配置された4つのターゲット（0～3）から、最も短時間でクリックできるものを選ぶというものである。この問題はフィッツの法則に基づいており「ターゲットが大きいほど、またターゲットとカーソルが近いほど、ポインティング時間が短くなる」という関係を前提としている。さらに、問題文では「カーソルがディスプレイの端で止まることにより、実質的にはそこにあるターゲットが無限大のサイズを持つ」という重要な条件が示されている。

　これらの条件に基づけば、公式解答であるターゲット2が正解となる。その理由は、まず画面の端や隅に配置されたターゲット2と3が「実質的に無限大のサイズを持つ」と見なされ、有限サイズのターゲット0と1よりも短時間でクリックできるためである。その上で、ターゲット2の方がターゲット3よりもカーソルからの距離が短いことから、最も短時間でクリックできると判断される。

　しかし、この解答に対してソーシャルメディア上ではさまざまな疑問が投稿された。論文では、これらの疑問を4つの観点から整理し、考察を行っている。

　第1の疑問は、ターゲットサイズが無限大の場合、移動時間は距離に関係なく0になってしまうのではないかというものである。しかし、フィッツの法則の理論的解釈によれば、ターゲットサイズが無限大の場合でも移動時間は一定の基本時間に収束し、ゼロにはならない。また、実際の人間の動作を考慮した弾道的ポインティングモデルでも、移動時間は距離の平方根と1次関数の関係になることを示している。

　第2の疑問は、ターゲットの見た目のサイズの影響についてである。ターゲット2と3は実質的に無限大のサイズを持つとされるが、画面上での見た目のサイズが異なることが影響しないのかという疑問である。

　先行研究の実験結果によれば、画面端まで伸びているターゲットの場合、見た目のサイズが異なっていても同じ時間でクリックでき、サイズによる有意差は見られなかった。ただし、これは特定のサイズ範囲内での結論であり、極端に小さいサイズについては未検証である。